Averaging Filter와 Gaussian Filter

Averaging Filter는 이미지의 특정 영역(이웃한 픽셀들)의 값을 평균 내서 중심 픽셀의 값을 대체하는 필터다.

이렇게 하면 이미지가 부드럽게 변하면서 노이즈가 줄어든다.

 

필터 마스크가 덮고 있는 영역 내의 모든 픽셀 값의 평균을 계산한다.

예를 들어, 3x3 크기의 마스크를 사용한다면, 9개의 픽셀 값을 더한 후 9로 나눈 값을 중심 픽셀 값으로 설정하는 거다.

 

이 필터는 Low Pass Filter라고도 불린다.

고주파 성분(즉, 급격한 밝기 변화)을 억제하고, 저주파 성분(즉, 서서히 변하는 밝기)을 남기기 때문에 이렇게 불린다.

그래서 이미지의 세부 디테일이 줄어들면서 부드럽게 처리된다.

이미지의 모든 픽셀에 대해, 그 픽셀이 포함된 이웃 영역의 평균 값으로 픽셀 값을 대체한다.

이 과정을 이미지의 모든 픽셀에 반복해서 적용하는 거다.

 

장점으로는 이미지의 랜덤 노이즈를 줄이는 데 효과적이다.

노이즈가 평균 값에 의해 상쇄되기 때문이다.

 

단점으로는 이미지가 흐려진다.

평균을 내다 보니 원래 선명했던 부분도 부드럽게 변하니까 이미지의 엣지나 디테일이 흐릿해진다.

 

다음은 Averaging Filter의 예다

 

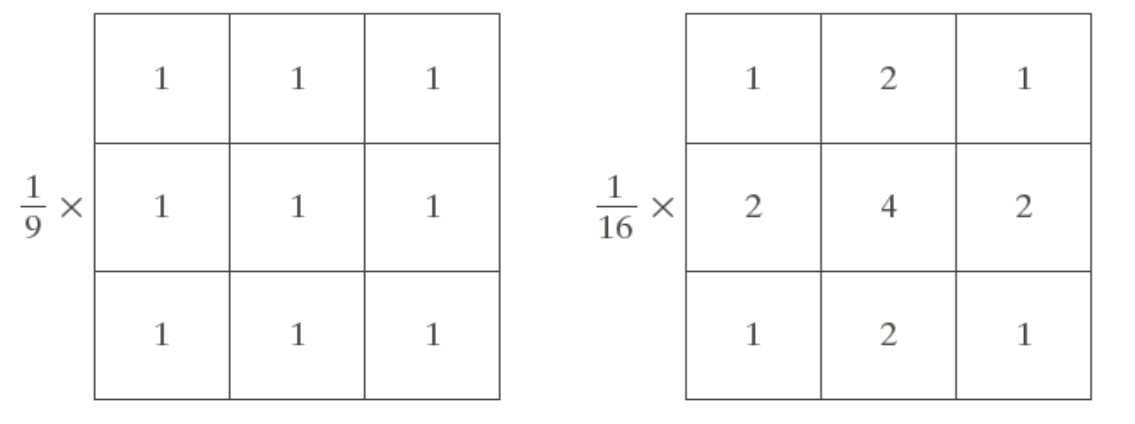
두 가지 3x3 필터 마스크가 있다.

 

첫 번째는 균일 필터로 모든 요소가 1이니 필터 값들을 모두 더하면 9가 된다.

그래서 이 마스크에 1/9를 곱해줘야한다. 이렇게 하면 각 요소의 값이 평균화된다.

 

두번째는 가우시안 필터로 가운데 값이 4, 주변 값이 2와 1인 필터다.

이 마스크는 중심 픽셀에 더 큰 가중치를 주는 방식으로, 가우시안 분포(종 모양 곡선)에 따라 가중치가 부여된다.

필터 값들을 모두 더하면 16이 되니까, 이 마스크에 1/16을 곱해줘야 한다.

중심에 가까운 픽셀 값이 더 중요하게 반영돼서 더 자연스럽게 블러링이 된다.

 

균일 필터는 모든 주변 픽셀을 동일하게 고려해서 평균 값을 계산하는 방식이다.

단순하면서도 효과적이지만, 이미지가 지나치게 부드러워질 수 있다.

 

가우시안 필터는 중심 픽셀에 더 많은 가중치를 부여해 좀 더 자연스러운 블러링을 제공한다.

이 필터는 노이즈를 줄이면서도 상대적으로 더 많은 디테일을 유지할 수 있다.

 

 

가우시안 필터에 대해서 더 자세히 알아보자

이 필터는 고주파 성분을 제거하고 저주파 성분만 남긴다.

즉 이미지의 세부 디테일을 줄이고 노이즈를 제거하는 역할을 한다.

 

다음은 가우시안 함수를 적용해서 만들어진 예제를 살펴보자

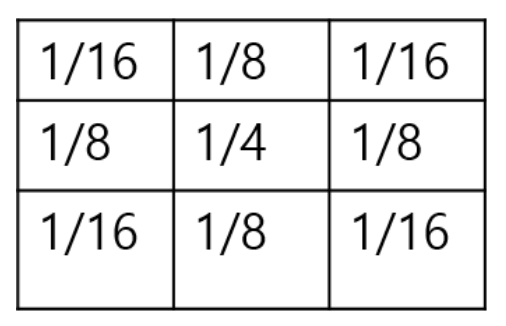
필터의 중심에는 가장 큰 가중치인 1/4가 있고, 주변으로 갈수록 가중치가 줄어들어 1/16이 된다.

이렇게 하면 중심에 가까운 픽셀일수록 더 많은 영향을 주고, 멀어질수록 영향이 적어져서 자연스러운 블러 효과를 만든다.

 

이번엔 가우시안 커널에 대해서 알아보자

가우시안 커널은 가우시안 필터를 적용할 때 사용하는 계수의 행렬이다.

이 행렬은 필터의 크기와 표준편차(σ, 시그마)에 따라 결정된다.

커널의 크기가 클수록 더 많은 주변 픽셀을 고려하게 되고, σ가 클수록 필터링 효과가 강해진다.

 

이 커널은 3x3 크기의 작은 가우시안 필터를 나타낸다. 표준편차(σ)가 1인 경우로, 중심에 가까운 픽셀에 더 큰 가중치를 주고 있다.

커널의 중심 값이 가장 크고(0.204), 가장자리로 갈수록 값이 작아진다(0.075).

 

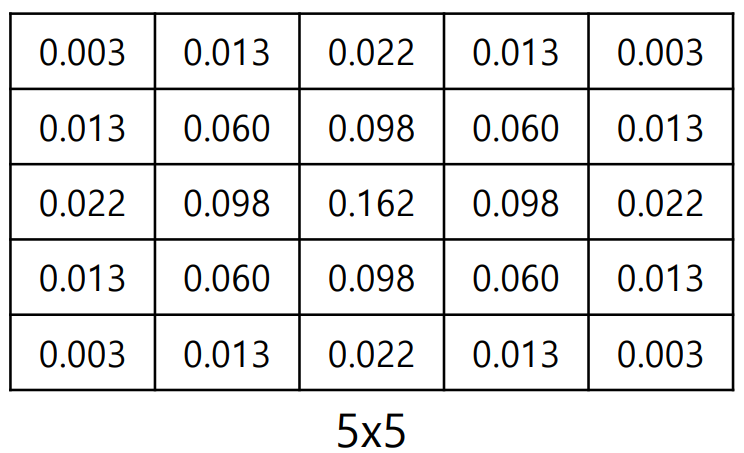
이 커널은 5x5 크기의 가우시안 필터다. 3x3 커널보다 더 넓다.

중심 값이 0.162로 가장 크고, 주변으로 갈수록 가중치가 줄어든다.

 

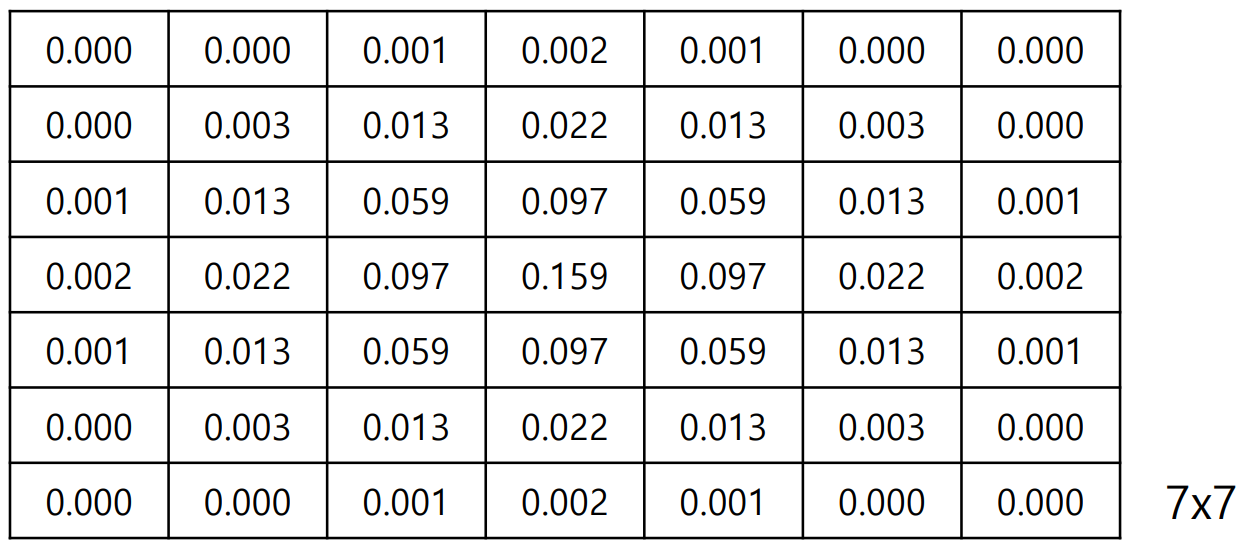
이 커널은 7x7 크기의 가우시안 필터다.

더 넓은 범위의 픽셀을 포함하며, 필터링 효과가 더 강하다.

중심 값이 0.159로 가장 크고, 주변으로 갈수록 값이 점점 작아진다.

3x3, 5x5, 7x7 가우시안 커널들은 가우시안 필터의 크기와 σ=1인 경우를 보여주고 있다.

 

σ(시그마)의 의미는 무엇일까

σ는 필터의 표준편차로, 필터의 강도를 조절한다.

σ가 커질수록 블러링이 더 강해진다, 노이즈 제거에 효과적이지만 이미지의 디테일이 손실될 수 있다.

반면 σ가 작으면 필터링 효과가 약해지고 노이즈 제거는 덜하지만 이미지의 디테일은 잘 유지된다.

 

 

이제 이산화된 가우시안 커널(Discretized Gaussian Kernel)에 대해서 알아보자

여기서 중요한 건, 가우시안 필터를 실제로 사용할 때 정수 값으로 이산화 하는 과정이 어떻게 이루어지는지 보여준다는 거다.

 

가우시안 커널 이산화란?

가우시안 커널은 원래 연속적인 가우스 함수를 기반으로 계산된다.

그런데 컴퓨터는 연속적인 값을 처리할 수 없으니까, 실제로는 이 값을 이산화(즉, 정수로 변환)해야 한다.

이산화된 가우시안 커널은 정수 값으로 구성되어 있어 계산이 더 간단하고 빠르게 이루어진다.

 

 

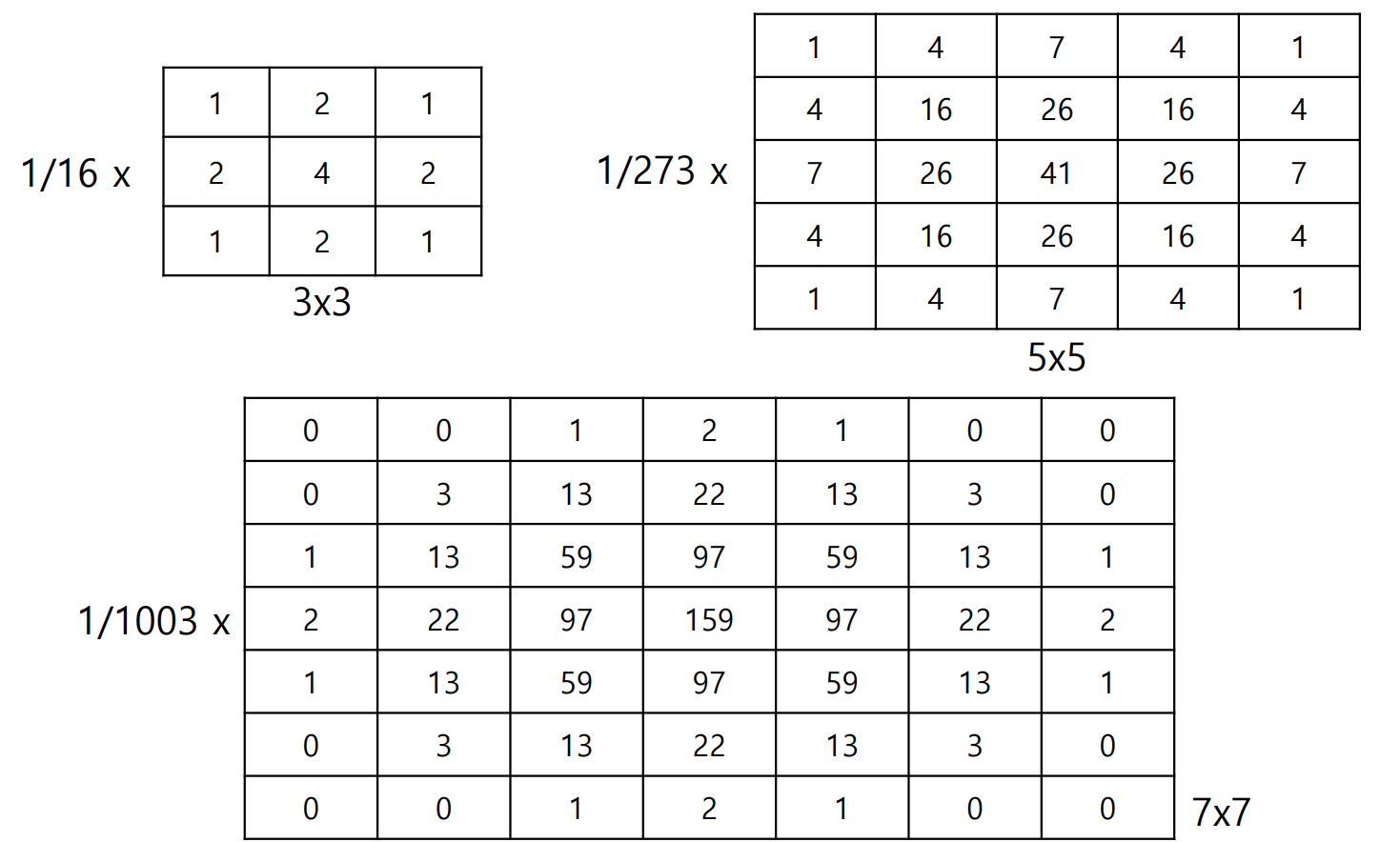
다음은 이산화한 커널들의 모습이다.

이 값들은 가우스 함수의 값을 정수로 변환한 결과다.

 

커널 내 모든 요소의 합이 1이 되도록 정규화해야 한다.

그러면 전체 이미지의 밝기를 유지하면서 필터링할 수 있다.

커널이 클수록 이미지의 더 넓은 영역을 참조하지만, 그만큼 더 부드러운 효과가 생겨 디테일이 손실될 수 있다.