두 변수 간의 관계 측정

두 변수 간의 관계를 측정하는 방법으로 크게 두 가지가 있다.

 

1. 공분산(Covariance)

공분산은 두 변수가 어떤 방향으로 변하는지를 나타내는 지표다.

만약 두 변수가 같은 방향으로 변하면 공분산은 양수고, 반대 방향으로 변하면 공분산은 음수다.

하지만 공분산은 단위에 의존하니까, 단위가 달라지면 해석이 어렵다.

 

샘플에서 공분산을 계산하려면 이 공식을 쓴다.

 

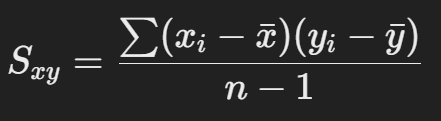
• xi​: 첫 번째 변수의 각 데이터 값.
• xˉ: 첫 번째 변수의 평균.
• yi​: 두 번째 변수의 각 데이터 값.
• yˉ: 두 번째 변수의 평균.
• n: 샘플의 개수.

각각의 x값에서 평균을 빼고, 각각의 y값에서도 평균을 빼서 그 두 값을 곱한 후 다 더하고 그 값을 샘플 수 - 1로 나누면 샘플의 공분산을 구할 수 있다.

 

모집단에서 공분산을 구할 땐 아래 공식을 사용한다.

 

 

• μx​: 첫 번째 변수의 모집단 평균.
• μy: 두 번째 변수의 모집단 평균.
• N: 모집단의 크기.

 

여기선 샘플 대신 모집단의 평균을 사용하고, 샘플의 개수 대신 전체 모집단의 개수로 나눠준다.

 

만약 Sxy 값이 양수라면, 이는 두 변수가 같은 방향으로 움직인다는 의미다.

즉, 점들이 1사분면과 3사분면에 더 많이 분포해 있다는 거다.

이렇게 되면 양의 선형 관계가 있는 걸로 해석할 수 있다.

 

공분산 값은 두 변수 간의 관계를 보여주긴 하지만, 단위에 영향을 받는다는 단점이 있다.

예를 들어 키를 미터(meter)로 측정하느냐 센티미터(cm)로 측정하느냐에 따라 공분산 값이 달라진다. 미터로 재면 공분산 값이 작고, 센티미터로 재면 더 커진다. 하지만 두 변수 사이의 관계 자체는 변하지 않는다.

공분산의 이런 문제를 해결해주는 게 상관계수다.

 

2. 상관계수(Correlation Coefficient)

상관계수는 공분산을 표준화한 값이다. 그래서 단위에 영향을 받지 않는다.

-1부터 1 사이의 값을 가지며, 

1에 가까울수록 두 변수가 강하게 양의 상관관계를 가짐을 의미하고,

-1에 가까울수록 두 변수가 강하게 음의 상관관계를 가짐을 의미한다.

0에 가까우면 두 변수 간에 상관관계가 거의 없다는 뜻이다.

 

다만, 주의사항으로는 상관관계는 두 변수 간의 선형 관계를 측정하는 거지 인과관계를 의미하는게 아니다.

 

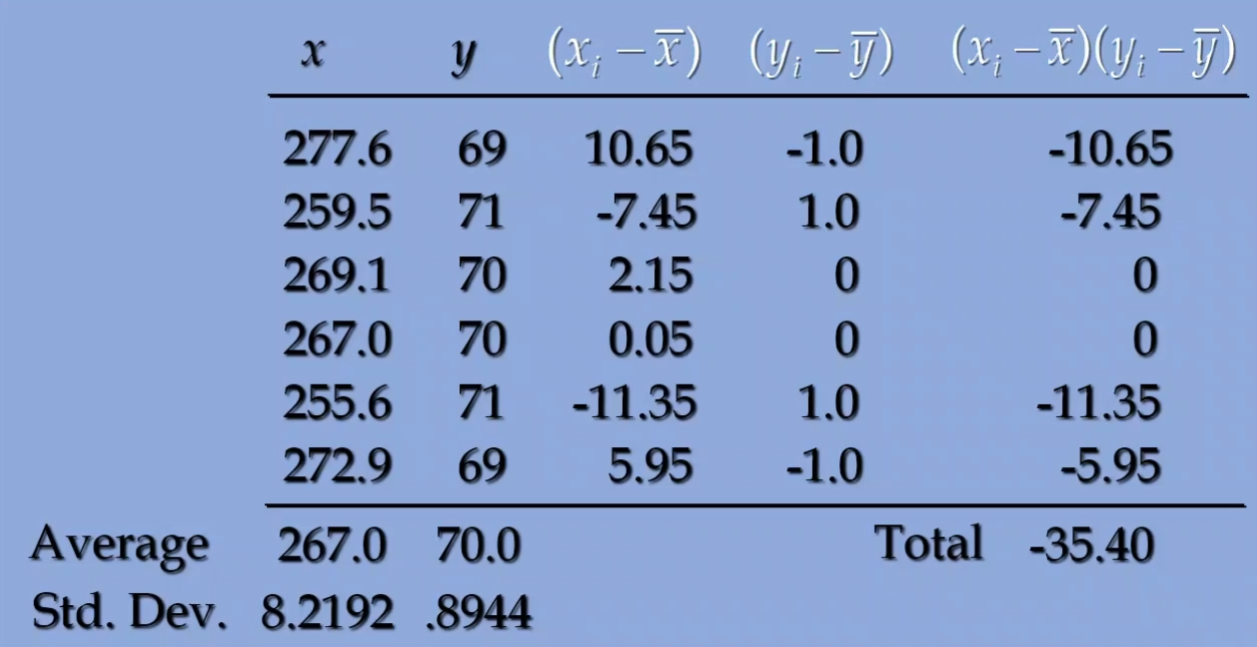
다음과 같은 골프 연구 자료가 있다고 해보자

x는 골프 공이 날아간 거리, y는 날아간 거리에 따른 점수(예를 들어 퍼팅 횟수)라고 해보자

각각의 평균은 267, 70이다.

(xi−xˉ)는 각 x 값에서 x의 평균(267.0)을 뺀 값이다.

y도 마찬가지

 

(xi​−xˉ)(yi​−yˉ​)는 각각의 편차를 곱한 값이다. 

예를 들어, 첫 번째 행에서는 10.65×(−1.0)=−10.65가 나왔다.

이 값들의 합계가 총 -35.40이다. 이 값을 사용해서 공분산을 구할 수 있다.

 

공분산을 구할 때는, 이 값들의 총합을 데이터 포인트 개수 - 1로 나눈다.

데이터 포인트는 6개니 5가 된다.

따라서 공분산은 -35.40/5 = −7.08다.

 

이제 상관계수를 계산해보자면

각 표준편차가 Sx​=8.2192, Sy=0.8944이니까, 

상관계수 r = -7.08/( 8.2192 * 0.8944 ) = −0.967 정도가 된다.

 

결론으로는 공분산이 음수니까 두 변수는 반비례 관계가 있단 뜻이다.

즉, 골프 공이 멀리 날아가면 퍼팅 횟수는 줄어든다는 거다.

상관계수가 -0.967인 걸 보면, 두 변수 간의 음의 상관관계가 아주 강함을 알 수 있다.