-
상자 그림(Box Plot)이란?경제 2024. 9. 14. 20:43
상자 그림(Box Plot)은 주로 데이터의 분포와 극단값(outliers)을 쉽게 확인할 수 있고, 상자 그림은 사분위수로 만들어져 있다.
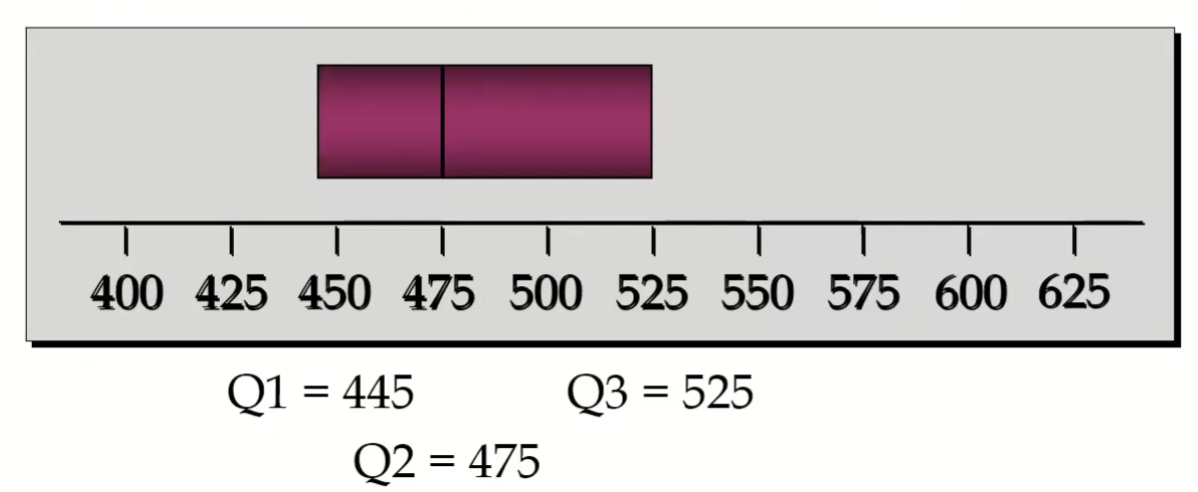
상자의 끝은 1사분위수(Q1)와 3사분위수(Q3) 위치를 나타낸다.
Q1 (첫 번째 사분위수) = 445
Q3 (세 번째 사분위수) = 525
상자 안에 있는 세로선은 중앙값(중위수, Q2)을 나타낸다.
Q2 (중앙값, 메디안이라고 부른다) = 475
상자 그림(Box Plot)에서 Outlier를 판별하는 기준은 다음과 같다.
1. IQR(Interquartile Range) 계산
IQR은 Q3 - Q1, 즉 3사분위수와 1사분위수의 차이다.
여기서는 525 - 445 = 80이 된다.
2. Lower Limit (하한선)
하한선은 Q1에서 1.5배의 IQR을 뺀 값이다.
공식은 Q1 - 1.5 * IQR
여기서 445 - 1.5 * 80 = 445 - 120 = 325이 나온다.
즉, 325보다 작은 값은 이상치로 간주될 수 있다.
3. Upper Limit (상한선)
상한선은 Q3에 1.5배의 IQR을 더한 값이다.
공식은 Q3 + 1.5 * IQR
여기서 525 + 1.5 * 80 = 525 + 120 = 645
즉, 645보다 큰 값도 이상치로 간주될 수 있다.
아무튼 325 미만 645 초과인 값이 있으면 이상치가 있다고 할 수 있다.
상자 그림에서 나오는 수염(whiskers)에 대해 알아보자
수염은 상자 그림에서 상자 끝에서 가장 작은 값과 가장 큰 값으로 이어지는 선을 말한다.
이 선은 데이터 세트에서 이상치(outliers)로 간주되지 않는 값들까지 연결한다.

왼쪽 수염: Q1(첫 번째 사분위수, 445)에서 가장 작은 값(이 경우 425)까지 이어진다. 이 값은 하한선 안에 들어가니까 이상치가 아니다.
오른쪽 수염: Q3(세 번째 사분위수, 525)에서 가장 큰 값(이 경우 615)까지 이어진다. 이 값도 상한선 안에 들어가니까 역시 이상치가 아니다.
425는 이 데이터에서 가장 작은 값이지만 하한선(325)보다 크니까 이상치가 아니다.
615는 가장 큰 값이지만 상한선(645)보다 작으니까 이상치가 아니다.
결론적으로, 이 데이터에서는 이상치가 없고, 모든 값들이 수염 안에 잘 포함되어 있다.
'경제' 카테고리의 다른 글
상관관계(Correlation)와 인과관계(Causation)의 차이 (0) 2024.09.14 두 변수 간의 관계 측정 (0) 2024.09.14 Outlier란? (0) 2024.09.14 Empirical Rule (경험적 규칙) (0) 2024.09.14 Chebyshev's Theorem(체비셰프의 정리) (3) 2024.09.14