초기하 분포와 포아송 분포

초기하 분포(Hypergeometric Distribution)는 비복원 추출에서 사용된다.

즉, 샘플을 뽑을 때 뽑힌 것을 다시 넣지 않는 실험에서, 특정 사건이 발생할 확률을 구하는 데 쓰인다.

예를 들어, 상자에 들어있는 검은 공과 흰 공 중에서 몇 개를 뽑았을 때 검은 공이 몇 개 나올 확률을 구하는 거다.

 

초기하 분포는 아래와 같은 상황에서 적용된다.

 

• 모집단에 성공/실패 두 가지 분류가 존재함
• 샘플을 복원하지 않고 추출함
• 모집단의 크기와 추출된 샘플 크기가 고정됨

초기하 분포의 확률을 구하는 공식은 다음과 같다.

 

 

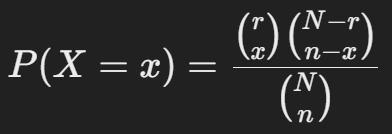
N: 모집단의 크기 (전체 공의 개수)

r: 모집단에서 성공의 수 (검은 공의 개수)

n: 샘플 크기 (뽑은 공의 개수)

x: 샘플에서 성공의 수 (검은 공이 나오는 횟수)

 

예를 들어, 상자에 검은 공 5개와 흰 공 10개가 있는 상황에서, 3개의 공을 뽑았을 때 검은 공 2개가 나올 확률을 구해보자

 

N=15 (전체 공의 수)

r=5(검은 공의 수)

n=3(뽑은 공의 수)

x=2(검은 공 2개 나올 확률을 구할 때)

 

초기하 분포 공식을 적용하면

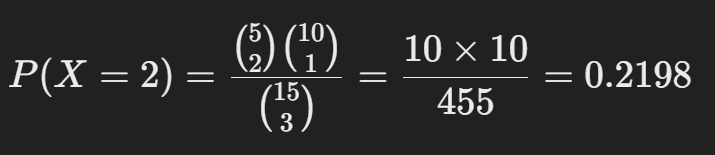
즉, 검은 공 2개가 나올 확률은 약 21.98%가 되는 거다.

초기하 분포는 복원하지 않는 실험에 사용되기 때문에, 각 번의 실험이 독립적이지 않다.

샘플을 뽑을 때마다 모집단에서 사라지기 때문에, 다음 샘플에서 나올 확률이 계속 달라진다.

 

---

포아송 분포(Poisson Distribution)는 특정 시간이나 공간 안에서 발생하는 사건의 수를 예측할 때 사용하는 분포다.

이 분포는 사건이 얼마나 자주 일어날지를 예측하는 데 매우 유용하다.

예를 들어, 은행에 몇 명의 고객이 한 시간 내에 방문할지를 예측할 수 있다.

 

포아송 분포는 아래와 같은 상황에서 적용된다.

 

• 사건이 독립적으로 발생함
• 일정한 시간이나 공간 내에서 사건 발생 빈도를 예측함
• 주어진 시간 동안 사건이 발생할 확률이 일정함

포아송 분포는 다음과 같은 수식으로 표현된다.

 

 

λ: 주어진 시간 또는 공간 내에서 발생하는 사건의 평균 횟수

x: 발생한 사건의 수

e: 자연 상수(약 2.718)

 

예를 들어, 병원 응급실에 평균적으로 한 시간에 4명이 방문한다고 하자. 한 시간 동안 2명의 환자가 방문할 확률을 구해보면

 

 

λ=4 (평균 방문자 수)

x=2(2명의 환자 방문 확률)

 

 

 

 

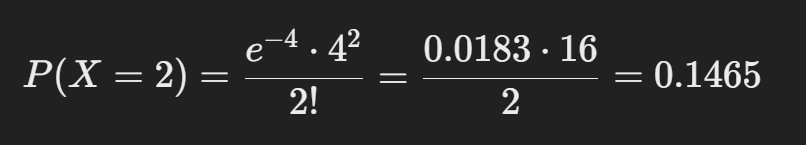
즉, 한 시간 동안 2명의 환자가 방문할 확률은 약 14.65%다.

 

포아송 분포는 사건이 독립적으로 일어나는 상황에서 주로 사용된다.

사건이 일정한 시간 또는 공간 안에서 발생하며, 그 사건의 평균 발생 횟수가 중요한 기준이 된다.

 

또한, 이항 분포에서 시도 횟수가 많고 성공 확률이 매우 작을 때 포아송 분포로 근사할 수 있다.

예를 들어, 100번의 시도 중에서 성공 확률이 0.01인 사건이 일어날 확률을 포아송 분포로 근사할 수 있다.

 

초기하 분포와 포아송 분포의 차이점은 

초기하 분포는 비복원 추출에서 사용된다. 샘플이 독립적이지 않다. 예를 들어, 공을 다시 넣지 않고 뽑는 상황

포아송 분포는 사건이 독립적으로 발생하는 상황에서 사용된다. 주로 시간이나 공간 내에서 발생하는 사건의 횟수를 예측하는 데 사용된다.

 

 

이제 이 초기하 분포와 포아송 분포의 실생활 적용 예시를 살펴보자

 

초기하 분포의 실생활 적용 예시

공장에서 제품을 무작위로 검사할 때 초기하 분포가 자주 사용된다.

예를 들어, 전체 제품 중 불량품이 몇 개 있는지 알고 있을 때, 10개의 샘플을 무작위로 뽑아 그 중 불량품이 몇 개 나올 확률을 구할 수 있다.

이때는 뽑은 제품을 다시 넣지 않기 때문에, 샘플이 독립적이지 않아 초기하 분포가 딱 맞다.

 

그리고 카드 덱에서 카드를 무작위로 뽑을 때도 초기하 분포를 적용할 수 있다.

예를 들어, 52장의 카드 중에서 에이스 4장이 있는데, 5장의 카드를 뽑았을 때 에이스가 몇 장 나올지 계산할 수 있다.

복원하지 않고 뽑는 것이므로 초기하 분포가 적합하다.

 

포아송 분포의 실생활 적용 예시

포아송 분포는 서비스 산업에서 고객의 도착 시간을 예측하는 데 자주 사용된다.

예를 들어, 한 시간 동안 카페에 평균 10명의 고객이 방문한다고 하면, 특정 시간대에 몇 명의 고객이 방문할지 예측할 수 있다.

이는 고객들이 독립적으로 도착하고, 시간당 평균 방문자 수가 일정하기 때문에 포아송 분포로 분석할 수 있다.

 

그리고 특정 지역에서 교통사고가 발생하는 횟수도 포아송 분포를 통해 예측할 수 있다.

예를 들어, 한 달에 평균 3건의 사고가 발생하는 도로에서 다음 달에 몇 건의 사고가 발생할지 예측하는 데 사용할 수 있다.

사고 발생이 독립적이고, 일정 시간 동안의 평균 빈도가 중요하기 때문에 포아송 분포가 적합하다.

 

다시 요약하자면..

초기하 분포는 비복원 추출 상황에서 성공과 실패라는 두 가지 결과를 예측할 때 사용되고 품질 관리나 카드 게임처럼, 샘플을 뽑을 때 복원하지 않고 뽑는 경우에 적용되며, 샘플링의 결과가 독립적이지 않은 특징이 있다.

포아송 분포는 특정 시간이나 공간 내에서 발생하는 사건의 빈도를 예측하는 데 사용된다. 

고객의 방문 시간이나 교통사고 발생 횟수처럼, 사건이 독립적으로 발생하고, 그 사건이 일어나는 평균 빈도가 일정할 때 적용된다.